Автор(ы) статьи: КОЗОДАЕВА Н.В.
Раздел: ИСТОРИЧЕСКАЯ КУЛЬТУРОЛОГИЯ
Ключевые слова:

архитектурная форма, архитектурная среда, система мер, пропорция, золотое сечение, гармония, математика архитектуры.

Аннотация:

В данной статье подробно рассматриваются существовавшие системы мер от Древней Руси до ХХ века. Приводятся математические исследования пропорционального строя памятников архитектуры, основы музыкальной аналогии в архитектуре.

Текст статьи:

В разных местах земного шара, в разные времена и у разных народов эталоны длины объединял один главный признак: все они происходили от человеческого тела. Антропометрические меры  обладали ценнейшим для архитектуры качеством, о котором, к сожалению, с введением метрической системы мер забыли, но к которому в ХХ веке вернулся Ле Корбюзье. Дело в том, что антропометрические меры в силу своего происхождения соразмерны человеку и поэтому удобны для конструирования искусственной среды обитания людей – архитектурных сооружений. Более того, в таких «очеловеченных» мерах заложены пропорции, отобранные самой природой, такие, как деление пополам, золотое сечение, функция золотого сечения. Следовательно, в антропометрических мерах естественным образом заложена гармония природы.

Основной строительной мерой в Древней Руси была сажень, равная размаху рук в стороны. Сажень делится на 2 полусажени, полусажень – на 2 локтя – расстояние от кончиков пальцев до локтя, локоть – на 2 пяди – расстояние между вытянутыми в противоположные стороны большим пальцем и мизинцем. Однако чем пристальнее историки изучали древнерусские летописи, тем больше становилось саженей, затем их число превысило десять и появилась необходимость систематизировать древнерусскую систему мер. Это сделали историк, академик Б.А.Рыбаков и архитектор И.Ш.Шевелев.

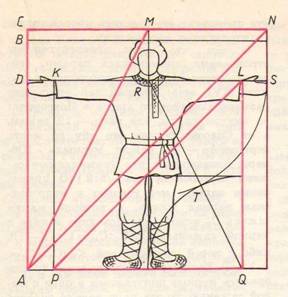
Рис.1 Основные древнерусские меры длины и геометрическая взаимосвязь между ними.

Основой антропометрических мер был рост человека а. Главной из всех видов саженей является мерная, или маховая, сажень С_м, которая равна размаху рук человека в стороны. Изучение пропорций человеческого тела показывает, что С_м=1,03а. Другой важной мерой у всех народов являлся двойной шаг, который равен высоте туловища от стоп до основания шеи. Последнее расстояние, как мы знаем, равно . Таким образом, двойной шаг, или малая (тмутараканская) сажень, . Но стоит отметить, что отношение этих двух основных размеров: . Следовательно, малая сажень С_т относится к мерной С_м как сторона двойного квадрата к его диагонали без малой стороны: . Из предыдущей формулы ясно, что отношение мерной полусажени С_м/2 к малой сажени С_т равно золотому сечению: . Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т.е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.

Построив квадраты на малой С_т и мерной С_м саженях и проведя в них диагонали, мы получаем еще два типа саженей: косую новгородскую сажень  и великую косую сажень . В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что . Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети С_ч, равная диагонали АМ половины квадрата, построенного на мерной сажени С_м. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что , откуда , т.е. отношение сажени без чети С_ч к мерной сажени С_м равно функции золотого сечения (рис.1).

Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г., позволила уточнить их размеры. Новгородские меры ХII века соответствуют росту человека: а=170,5 см. Тогда См==175,6 см, Ст=142,1 см, Кн=200,9 см, Кв=248,3 см, Сч=196,3 см. Если же рост человека принять равным 6 греческим футам:  см, то для основных саженей (мерной и малой) получим значения: См=190,8 см и Ст=154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.

О том, что меры древнерусскими строителями применялись парами, свидетельствует, например, новгородская грамота XVI века, которая так описывает размеры Софийского храма в Новгороде: «а внутри главы, где окна, — 12 сажен, а от Спасова образа ото лбу до моста церковного – 15 сажен мерных». (Обмеры показывают, что упоминаемые сажени соотносятся как .) О применении парных мер говорит новгородская мерная трость, в которой малая сажень Ст использовалась либо в паре с мерной саженью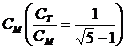, либо с косой новгородской 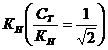. Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение . Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата [1].

Неповторимая прелесть, «нюанс», который присущ архитектурным памятникам древнерусских мастеров подчинялся  простой формуле, записанной в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: «А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки – как мера и красота скажет…»

Рассмотрим пропорциональный строй древнерусского шедевра архитектуры — церковь Покрова на Нерли.

Согласно архитектору Шевелеву, в основе пропорционального строения церкви Покрова лежит отношение сажени без чети к мерной сажени, которое является функцией золотого сечения , а сам план церкви был построен следующим образом (рис.2). В начале размещался прямоугольник длиной 3 сажени без чети и шириной 3 мерных сажени, который очерчивал столбы, несущие барабан и своды. Поскольку , то стороны этого прямоугольника относятся к функции золотого сечения, а сам прямоугольник является почти квадратом, или, в терминологии Жолтовского, «живым квадратом». Проведя в исходном прямоугольнике диагонали, зодчий получал центр храма, а отложив на диагоналях от вершин к центру по 1 мерной сажени, — подкупольный прямоугольник и размеры несущих столбов. Так было построено ядро плана, определявшее все дальнейшие горизонтальные и вертикальны размеры сооружения. Мерная сажень строителей церкви Покрова равнялась См=1,79 м.

В построении четверика храма явно виден принцип приблизительной симметрии, который так часто встречается в природе и искусстве. Можно указать и на более мелкие членения храма, относящиеся в функции золотого сечения, т.е. в отношении сажени без чети к мерной сажени. Например, каменный поясок, венчающий колончатый фриз, который охватывает всю церковь и является ее важной архитектурной деталью, делит высоту четверика в функции золотого сечения [1].

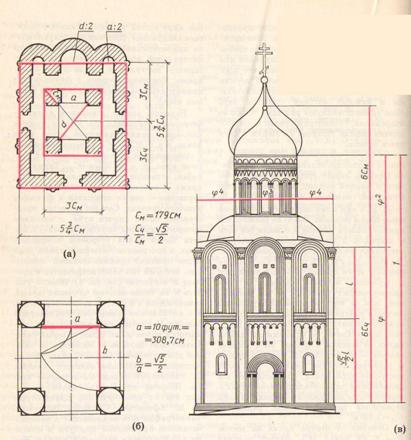
Рис. 2 Пропорции церкви Покрова Богородицы на Нерли. а) Построение плана с помощью парных мер по Шевелеву. б) Геометрическое построение ядра плана по Афанасьеву. в) Некоторые пропорциональные членения западного фасада

Рассмотрим  ихнографию храма Покрова на Нерли, какой ее видит знаток древнерусской архитектуры К.Н. Афанасьев. Согласно Витрувию, «ихнография есть надлежащее и последовательное применение циркуля и линейки для получения очертаний плана». Как считает Афанасьев, исходным размером церкви Покрова является меньшая сторона подкупольного прямоугольника, равная 10 греческим футам: а=10 греч.фут. = 308,7 см. Тогда большая сторона подкупольного прямоугольника получается как диагональ двойного квадрата со стороной а/2. Таким образом, подкупольный прямоугольник является «живым квадратом», стороны которого соотносятся в функции золотого сечения. Толщина столбов определяется отношением золотого сечения к модулю а/2. Дальнейшие построения ясны из рисунка (рис.2). Так строится ядро плана. Остальные размеры плана получаются аналогичными построениями, опираясь в основном на модуль а/2 [2].

Заметим, что вместе с функцией золотого сечения закон золотого сечения также определяет пропорциональный строй церкви Покрова. Это неудивительно, ибо данные отношения связаны геометрией двойного квадрата. Как установил Афанасьев, закону золотого сечения подчинены прежде всего главные вертикали храма, определяющие его силуэт: высота основания, равная высоте тонких колонок четверика, и высота барабана. Диаметр барабана относится к его высоте также в золотой пропорции. Эти пропорции видны с любых точек зрения. Переходя к западному фасаду, ряд золотого сечения можно продолжить: плечи храма относятся к диаметру барабана в золотой пропорции. Итак, принимая высоту белокаменной части церкви (от цоколя дол купола) за единицу, мы получаем ряд золотого сечения: который определяет силуэт архитектурного сооружения. Этот ряд можно продолжить и в более мелких деталях.

Можно сделать вывод, что непостижимая, казалось бы, гармония храма Покрова подчинена математически строгим законам сечения – «живым квадратам», а ее силуэт определяется рядом золотого сечения [3].

Существует еще один прекрасный пример гимна архитектурной гармонии — храм Вознесения в Коломенском (рис. 3).

Рис.3 Церковь Вознесения в селе Коломенском (ныне Москва). 1532. Шедевр древнерусского зодчества, один из первых каменных шатровых храмов на Руси.

Соразмерности храма с предельной ясностью определены двумя парными мерами: горизонтальные – малой (тмутараканской) саженью Ст и косой новгородской саженью 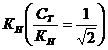, вертикальные – малой саженью Ст и мерной саженью 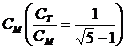и их комбинацией , дающей золотое сечение.

В основу плана церкви Вознесения положен квадрат ABCD сос тороной в 10 малых сажень: а=АВ=10Ст. Ясно, что диагонали квадрата равны 10 косым новгородским саженям: . Так с помощью парных мер Ст и Кн осуществлялся контроль правильности построения исходного квадрата. Окружность радиуса R=5Кн, описывающая квадрат, определяет положение всех 12 наружных углов плана храма. Вписав через середины сторон в квадрат ABCD новый квадрат и сделав построения, мы получим внешний контур плана – 20-угольник. Выступающие над исходным квадратом части называются притворами, их ширина равна а/2=5Ст. Выразив радиус описанной окружности R в мерных саженях, строители получали сторону квадрата b, определяющего внутреннее пространство храма:

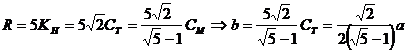. Разумеется коломенские мастера не вычисляли никаких радикалов. Они просто прикладывали мерную трость разными сторонами и автоматически переходили из одной меры в другую. План церкви построен. Выразим еще сторону квадрата с, охватывающего притворы: . Зная а, b, c,  легко выразить все остальные размеры плана и соотношения между ними (рис.4).

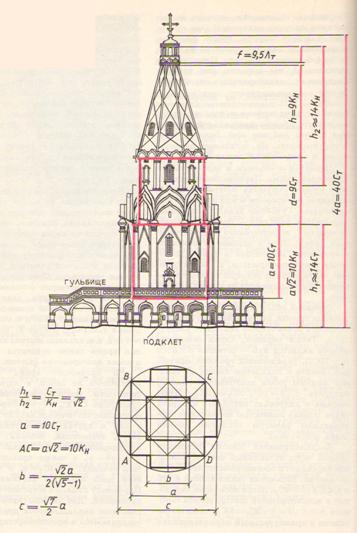
Рис.4 Пропорциональный строй церкви Вознесения в Коломенском (по Шевелеву).

Итак, мы видим как сторона ядра плана а, измеренная то малой саженью, то косой новгородской, рождает все главные вертикали храма. Заметим, что общая высота церкви от верха цоколя до яблока, на котором стоит крест, равна 4а=40С_т, т.е. также простейшим образом выражается через исходный размер а [1].

Новая метрическая система ведет свой отщет с 7 апереля 1795 г., в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины – метр – была примята 1/10000000 часть ¼ длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуры это имело самые серьезные последствия: «Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения и, если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении…Архитектура, построенная на метрических измерениях, сбилась с правильного пути» [4].

В условиях индустриализации строительные элементы необходимо было стандартизировать и унифицировать. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. «Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?» — спрашивал Ле Корбюзье[4]. И в 1949 г. он предлагает в качестве такого измерителя систему модульной унификации – модулор (рис.5).

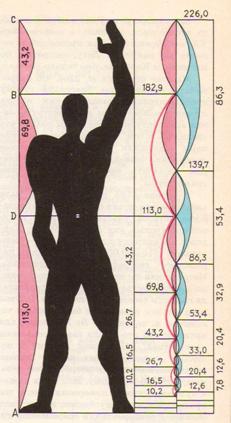
Рис.5 Модулор Ле Корбюзье. Рисунок Ле Корбюзье. «Модулор – это измерительный прибор, в основе которого лежат человеческий рост и математика» (Ле Корбюзье).

Идея построения модулора гениально проста. Модулор – это ряд золотого сечения:

…,	Ф-4	Ф-3	Ф-2	Ф-1	Ф0	Ф	Ф2	…
…,	0,146	0,236	0,382	0,618	1	1,618	2,618	…,

, умноженный на два коэффициента. Первый коэффициент k₁ равен росту человека; умножая на k₁, Корбюзье получает так называемый красный ряд. Второй коэффициент k₂ равен расстоянию от земли до конца поднятой руки человека (это большая сажень в древнерусской системе мер). При умножении на k₂ получается синий ряд. Осталось только выбрать числовые значения коэффициентов (рис.6). Желая примирить в модулоре английскую и французскую системы мер, а также следуя античной традиции, согласно которой рост человека равен 6 футам, Корбюзье взял в качестве k₁ 6 английских футов, т.е.  см. Значение k₂ принято равным 226,0 см. Так были получены красный ряд:

…,	26,7	43,2	69,8	113,0	182,9	295,9	478,8	…
…,	а-4	а-3	а-2	а-1	а0=к1	а1	а2	…,

И синий ряд:

…,	33,0	53,4	86,3	139,7	226,8	365,8	591,8	…
…,	b-4	b-3	b-2	b-1	b0=к2	b1	b2	…,

Значение k₂ было выбрано еще и так, чтобы между красным и синим рядами существовала простая связь: . Следовательно, синий ряд есть удвоение красного ряда.

Будучи геометрическими прогрессиями, члены обоих рядов модулора образуют цепь равных отношений: , т.е. в модулоре воплощается принцип гармонии: «из всего – единое, из единого – все». Благодаря аддитивному свойству золотого сечения «части» модулора сходятся в «целое». Наконец, абсолютные значения шкал модулора происходят от человека и потому хорошо приспособлены для проектирования архитектурной среды. Так, по мнению автора, модулор вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии [4].

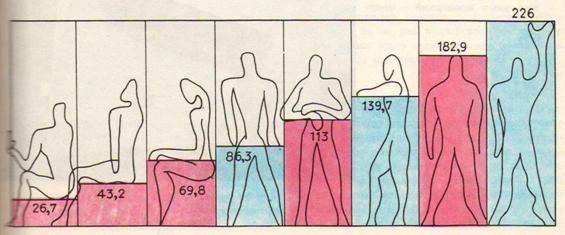
Рис.6 Числа красной и синей шкал модулора – действительные размеры, соответствующие определенным положениям тела человека. Рисунок Ле Корбюзье.

Однако в системе модулора был серьезный недостаток: размеры модулора оказались несоразмерными со средним ростом человека. Широкого распространения модулор так и не получил, а поиск совершенной гармонии продолжался.

Любую пропорциональную систему объединяет то, что сама система является основой, скелетом архитектурного сооружения. Именно это свойство модулора  Ле Корбюзье имел в виду Альберт Эйнштейн, давая ему восторженную оценку: «Модулор – это гамма пропорций, которая делает плохое трудным, а хорошее – легким».

Архитектурная форма абстрактна, поэтому в ней яснее, нежели в других искусствах, проявляются такие законы построения формы, как симметрия, пропорциональность, гармония, равенство, повторы частей и т.д. Лишенные внутренних законов построения, эти абстрактные формы будут лишены и тех внешних ориентиров, которые так необходимы при их восприятии. Именно объективным системным характером внутренних законов построения архитектурной формы объясняется то, что архитектрура вызывает сходные мысли у различных людей в различные временные периоды.

Архитектура во времени неизменна, а человек перемещаясь, меняя положение в среде, смотря на памятник архитектуры с разных точек зрения,в разное время суток, воспринимает архитектуру динамично.

Архитектура постигается зрителем во времени, процесс восприятия не связан никакой наперёд заданной последовательностью, зритель может приблизиться к архитектурному сооружению или отойти от него, остановиться. Любой просчет в пропорциональном строе будет постоянно довлеть на зрителя. Архитектура – это искусственная среда, в которой человеку предстоит жить и работать, и она должна доставлять ему только радость. Хотя, есть и обратные примеры. Стендаль признавался: «Я бы разучился смеяться через неделю, если бы жил в палаццо Арконати». Немало унылых памятников архитектурной какофонии окружают нас и сегодня. И все-таки по своей эстетической направленности архитектура призвана быть искусством положительных эмоций, она должна вбирать в себя все лучшие духовные ценности человечества и нести их людям. «Архитектура включает в себя всю культуру эпохи, в архитектуре проявляется дух времени», — писал Ле Корбюзье, чье высказывание дополняют слова Луначарского: «Всякому великому времени соответствует великая архитектура» [3,4].

Законы природы, законы гармоничного, целесообразного и прекрасного устройства мироздания описываются математикой. Вспомним слова Гейзенберга: «Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта».

Особенно ценно, что к тому же выводу о необходимости существования в основе архитектуры «объединяющего принципа формы» приходят не только представители естественных наук, но и деятели искусств. Вот слова архитектора, академика Щусева: «Наряду с меняющимися формами природы и жизни есть и нечто вечное, а именно – закон красоты и гармонии, который проявляется одинаково в жизни природы и человека. Именно этот закон дает возможность построить теорию пропорций и пластических форм».

Объединяющим принципом формы, который должен лежать в основе архитектуры становится математика – фундамент «закона красоты и гармонии», на котором строятся абстрактные формы архитектуры.

Интересно отметить тот факт, что в сознание архитекторов Возрождения прочно вошла музыкальная аналогия. Унивенрсальный характер математики, хорошо известные в музыке «математические законы красоты» (законы целочисленных консонантных отношений и законы среднепропорциональных) установили свои порядки: теоретические труды зодчих Возрождения определялись по большей части математическими разработками по теории музыки, а не трудами самих архитекторов.

Огромное влияние на зодчих Возрождения оказал трактат Витрувия «Десять книг об архитектуре». Ссылаясь на авторитет Витрувия, архитекторы Возрождения выдвинули тезис о том, что наиболее приятными для созерцания должны быть те прямоугольники, стороны которых относятся как числа в благозвучных (консонантных) интервалах, т.е. как октава 2:1, квинта 3:2, кварта 4:3, а а также большая 5:4 и малая 6:5 терции и их обращения – малая 8:5 и большая 5:3 сексты. В 1485 г. во Флоренции был издан трактат «Десять книг о зодчестве». Его автором был  представитель архитектуры Раннего Возрождения, итальянский ученый, писатель и музыкант Леон Баттиста Альберти. «Десять книг» Альберти было вторым после «Десяти книг» Витрувия всеобъемлющим сочинением по архитектуре. В нем мы читаем: «И конечно вновь и вновь следует повторить изречение Пифагора: «нет сомнений, что природа во всем остается себе подобной». Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и глаза, и дух чудесным наслаждением. Мы должны воспользоваться пропорциями, взятыми у музыкантов, кои величайшие мастера в этом виде чисел». Поскольку приятные слуху музыкальные интервалы описываются отношением целых чисел, то, согласно Альберти, и приятные глазу архитектурные формы также должны находиться в целочисленных «музыкальных» пропорциях [5].

В XVI веке архитектора Альберти поддержал математик Джероламо Кардано (1501-1576), известный сегодня как автор формулы решения кубического уравнения, которую, впрочем, как великую тайну ему открыл Никколо Тарталья (ок.1499-1557). Как истинный представитель точного знания Кардано утверждал, что приятные для слуха и глаза целочисленные (музыкальные) отношения являются таковыми, поскольку они легкопостижимы разумом. Авторство музыкальной аналогии в архитектуре Кардано также приписывал незыблемому авторитету Витрувия. Но следует отметить, что на самом деле интерес Витрувия к музыке ограничивался вопросами конструирования резонаторов для античных театров, а также правильной настройкой струн в катапультах и боевых машинах, которые находились в ведении архитекторов того времени. Правда, Витрувий дал в качестве прекрасных пропорций три «музыкальных» отношения 2:1, 3:2, 5:3. Но наряду с ними он рассматривал и такое отнюдь не музыкальное отношение, как отношение диагонали к стороне квадрата.

Огромную роль в развитии музыкальной аналогии в архитектуре сыграл трактат Северина Боэция «О музыке», который вобрал в себя все античные теории музыкальной гармонии и фактически сохранил их для потомков. Автор другого выдающегося трактата по математической теории музыки – итальянский композитор XVI века Джузеппе Царлино. Среди современников-музыкантов идеи Царлино должного признания не получили.Зато математические выкладки Царлино и его мысль о  том, что консонантные (приятные для слуха) интервалы получаются как среднее арифметическое и среднее гармоническое, запомнили современники-архитекторы и применяли их для получения «консонантных» (приятных для глаза) пропорций.

Музыкальная система пропорционирования нашла живой отклик в творчестве выдающегося итальянского архитектора Андреа Палладио (1508-1580) – автора трактата «Четыре книги об архитектуре». Созданные Палладио типы городского дворца, церкви, виллы благодаря своей завершенности, сочетанию строгой упорядоченности и пластики получили распространение не только в Италии XVI века, но и составили целое направление – палладионство – в европейском зодчестве XVII-XVIII веков.

Идея всепроникающей музыкальной гармонии, структурно-математическое понимание красоты, идея симметрии как неотъемлемого качества красоты наиболее полно воплощены Палладио в вилле Ротонда. С высоты птичьего полета в этом каноне архитектуры Ренессанса хорошо видны как поворотная симметрия 4-го порядка всего здания, так и зеркальная симметрия его фасадов, а также ощущается музыка простых целочисленных пропорций (рис.7).

Рис.7 Палладио. Вилла Ротонда в Виченце.1581. Воплощение идеи симметрии, математической строгости и музыкальных пропорций в архитектуре Ренессанса.

Вообще, убеждение в том, что архитектура – это наука и что красота здания определяется симметрией и математическими законами гармонии, можно считать главной аксиомой архитектуры Возрождения. Так как мыслители Возрождения были неоплатониками, они верили в то, что платонов гептахорд, который содержит все консонансы, определяет гармонию мироздания, а значит, и единую гармонию всех искусств, в том числе и архитектуры.

И все-таки Палладио был больше архитектором, нежели философом-неоплатоником. Именно поэтому Палладио включил прямоугольник, стороны которого равны стороне и диагонале квадрата, т.е. прямоугольник с иррациональным соотношением сторон , в список семи форм, рекомендуемых для планирования комнат (интервал тритона  является острейшим диссонансом в музыке и назывался «дьяволом в музыке»).

По его стопам пошли все архитекторы Возрождения. Для примера можно привести проект собора, выполненный Леонардо да Винчи и основанный на последовательности восьмиконечных звезд. Разбиение окружности на 8 равных частей порождает угол в 45 градусов, а восьмиконечная звезда – систему равнобедренных прямоугольных треугольников, т.е. треугольников с соотношением  (рис.8).

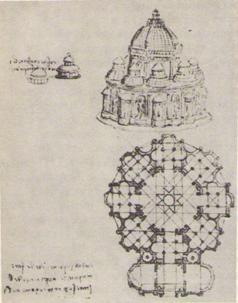
Рис.8 Леонардо да Винчи. План собора, основанный на правильной восьмиконечной звезде, обладает попоротной симметрией 8-го порядка и отнюдь «не музыкальной» системой пропорций

Но не смотря на непрочность музыкальной теории в архитектуре, она оставалась очень популярной и продолжала жить в творчестве архитекторов-палладианцев XVII и XVIII веков.

В 1830-1834 гг. немецкий физиолог Эрнст Вебер (1795-1878) на основании многочисленных экспериментов установил, что человек воспринимает не абсолютный, а относительный прирост силы раздражителя (света, звука, груза, давящего на кожу, и т.д.), т.е. , где R – сила раздражителя, dR – прирост этой силы. Каждый по своему жизненному опыту знает, что, например, электрическая лампочка, включенная днем, не вызывает никакой реакции, так как по отношению к солнечному свету прирост этой силы раздражения слишком мал (, так как R велико). Зато в темноте нас слепит даже зажженная спичка (здесь , так как R =0).

20 лет спустя немецкий физик, психолог, философ и писатель Густав Фехнер (1801-1887) математически обработал результаты экспериментов Вебера, т.е. на языке математики записал факт, установленный Вебером: приращение интенсивности ощущения dE пропорционально относительному приращению силы раздражения :

, здесь  а- коэффициент пропорциональности. Получилось простейшее дифференциальное уравнение, решая которое Фехнер нашел связь между интенсивностью ощущения Е и силой раздражения R, действующей на какой-либо огран чувств:  или , здесь R₀ – сила начального раздражения.

Эти формулы и есть математическое выражение основного психо-физического закона – закона Вебера-Фехнера.

Из этого закона можем сделать вывод, что нам будет приятно, если наши ощущения в процессе восприятия архитектуры будут нарастать равномерно, т.е. в арифметической прогрессии. Положим  (- разность арифметической прогрессии). Тогда согласно  вызывающая эти ощущения сила раздражения должна нарастать по закону 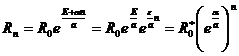, т.е. сила раздражения Rn должна нарастать в геометрической прогрессии со знаменателем  [3].

Напомним, что и ряд золотого сечения, и красная и синяя шкалы модулора Ле Корбюзье являются геометрическими прогрессиями. Следовательно, все эти «раздражители» наших органов чувств обеспечивают равномерное возрастание (или убывание) наших ощущений. Таким образом, именно закон Вебера-Фехнера, скорее всего, и является тем математическим законом, который лежит в основе основ архитектуры (шкала пропорциональностей), той «математикой», которая связывает и науку, и архитектуру.

 

Список литературы:

1.           Шевелев И.Ш. Принцип пропорции. – М.: Стройиздат,1986.

2.           Шевелев И.Ш., Марутаев М.А., Шмелёв И.П. Золотое сечение. — М.: Стройиздат,1990.

3.           Волошинов А.В. Математика и искусство.-М.: Просвещение,1992.-235 с.:ил. – ISBN 5-09-002705-6

4.           Ле Корбюзье. Архитектура ХХ века. – М.: Прогресс,1970.

5.           Альберти Л.-Б. Десять книг о зодчестве. – М.: ИАА,1935.